现在我们引入局部定义, 这将进一步增强我们的表达能力.
首先我们引入let形式, 它的一般句法是(let ((<var> <exp>) ...) <exp>). 而其语义, 可以将其视为句法糖来解释. (let ((x0 e0) ...) body)就等价于((lambda (x0 ...) body) e0 ...).
现在我们给出一个简单的例子.
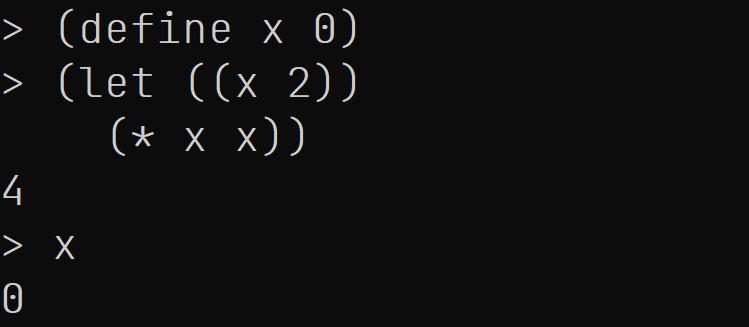
我们看到, let引入的绑定将顶层的绑定覆盖, 所以(let ((x 2)) (* x x))的值是4, 但是绑定不是赋值, 它不会修改外部的绑定, 所以当我们在REPL中对x求值时, 仍然得到0.
接着我们引入let*形式, 它和let有些类似, 实际上let*可以基于let定义.
let形式对于求值的顺序没有任何保证, 虽然现在看来它几乎不会造成任何问题, 因为我们还没有引入副作用. (let* ((x0 e0) (x1 e1) ...) body)等价于(let ((x0 e0)) (let* ((x1 e1) ...) body)), 而(let* () body)就等价于(let () body). 这使得let*具有明确的求值顺序, 即自左往右, 并且它逐次进行绑定.
现在我们给出一个简单的例子.
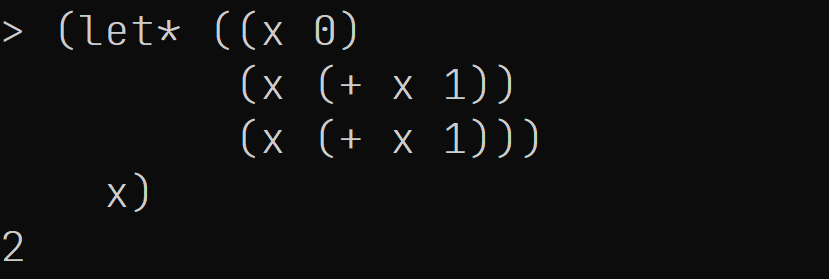
如果把这里的let*换成let, 则会产生异常, 因为lambda表达式的形式参数应该是互不相同的.
let和let*的语义很容易理解, letrec的语义则不太容易了. 但是, 如果我们仅仅将letrec用于引入(互)递归的过程, 则不会造成什么困难, 现在我们就给出一个例子.
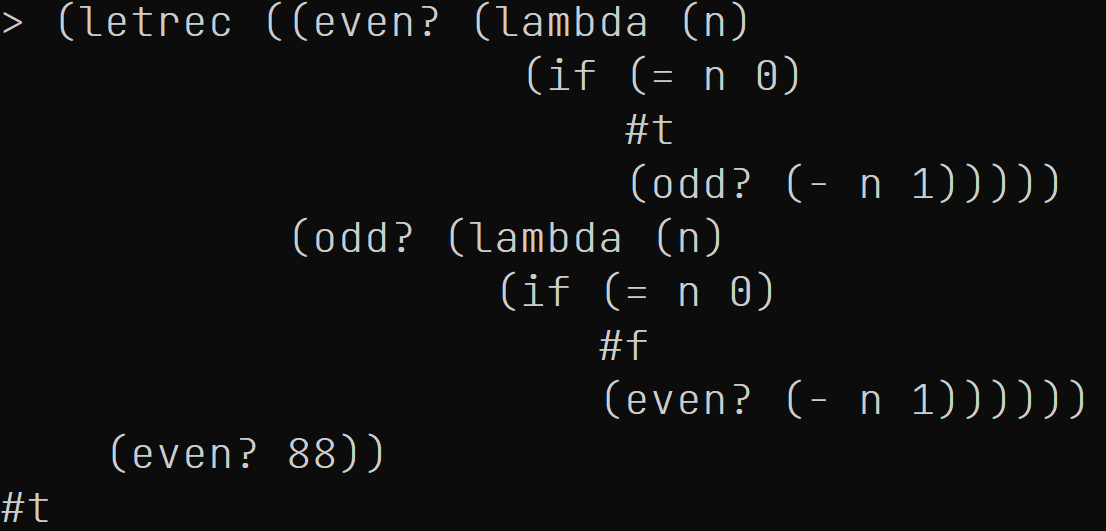
letrec和let不同的是, 它的各右支可以引用左侧的变量 (但是有一定的限制, 不过在只使用letrec引入递归的过程的情况下, 没有什么问题).
最后, 我们引入lambda内部的define, 它的作用范围仅限于lambda表达式的体.
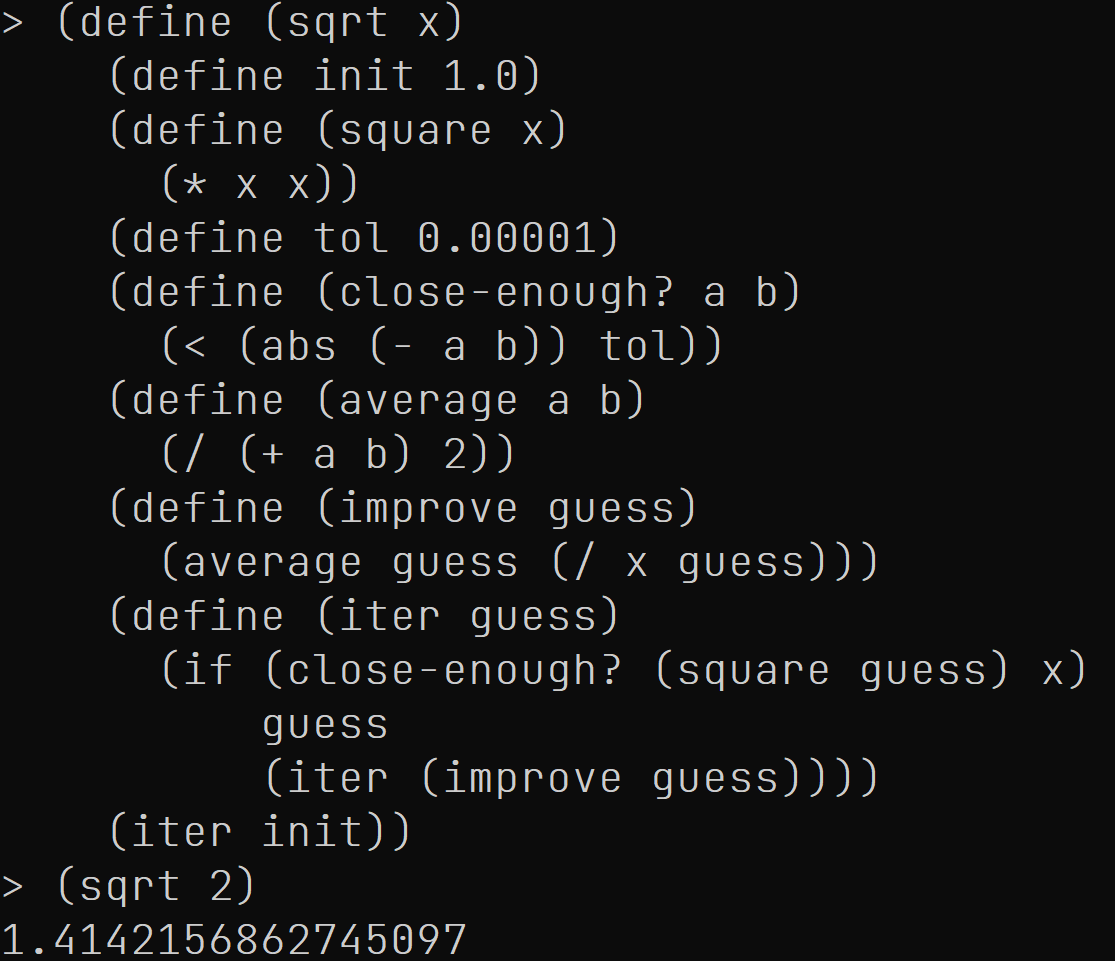
这是一个稍微复杂一点的例子, sqrt是一个利用迭代法求平方根的过程. 数学中的迭代法的大意是我们先给一个猜测值, 看它是否足够好, 如果不够好, 则改进它, 如此反复循环, 直至得到满意的值.
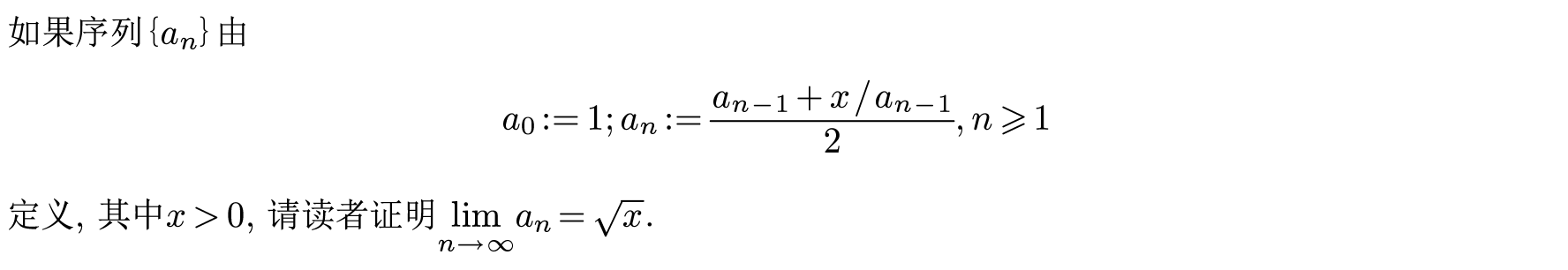
这是迭代法求平方根的依据.
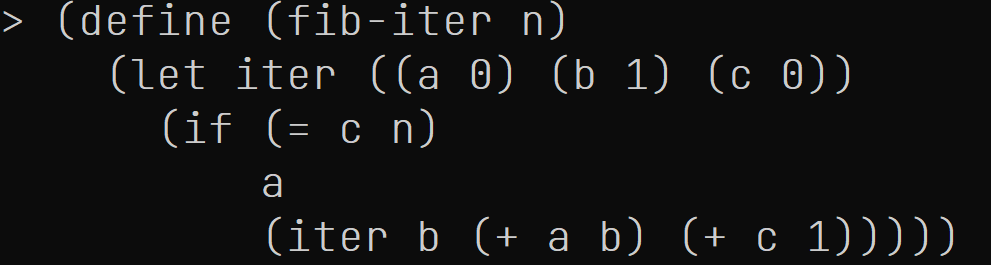
练习. 试说明, 以下过程也能正确计算Fibonacci数列的值, 也就是说, 对于每个自然数n, (fib-iter n)的值等于(fib n)的值.
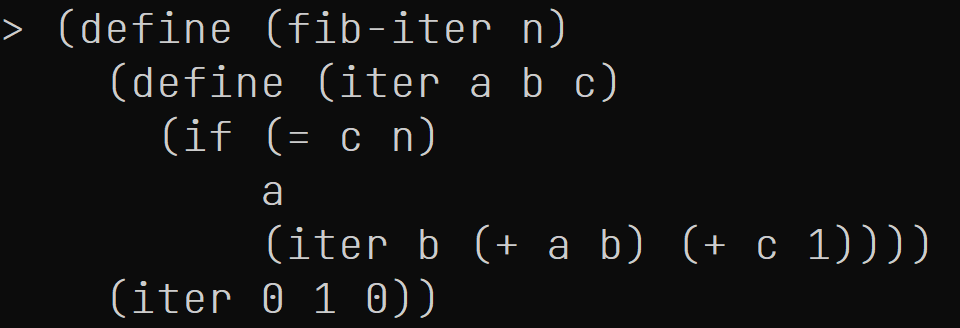
注记: 鉴于迭代 (不是迭代法) 这种模式经常出现, Scheme提供一种被称为"命名let"的句法糖, 比如说上面的fib-iter就可以改写为以下样式.